Errors in physical measurements

Error Propagation:
Errors in measurements translate into errors in everything calculated from that measurement. 


Example:
Small error in measuring the position with time of your car create errors in calculating the velocity and acceleration of your car.

Copy this example data set into excel:

Time    (sec)	Position (in)
0	0
1	2.5
2	10
3	22.5
4	40
5	62.5
6	86.25
7	107.5
8	126.25
9	142.5
10	156.25
11	167.5
12	176.25
13	182.5
14	186.25
15	187.5

Create new column in excel that calculate velocity and acceleration from the above data.

V2 = 2*(x2-x1)/(t2-t1) - V1

a = (v2-v1)/(t2-t1)

Answer check:  Your spreadsheet should look like this:

Insert two more columns:

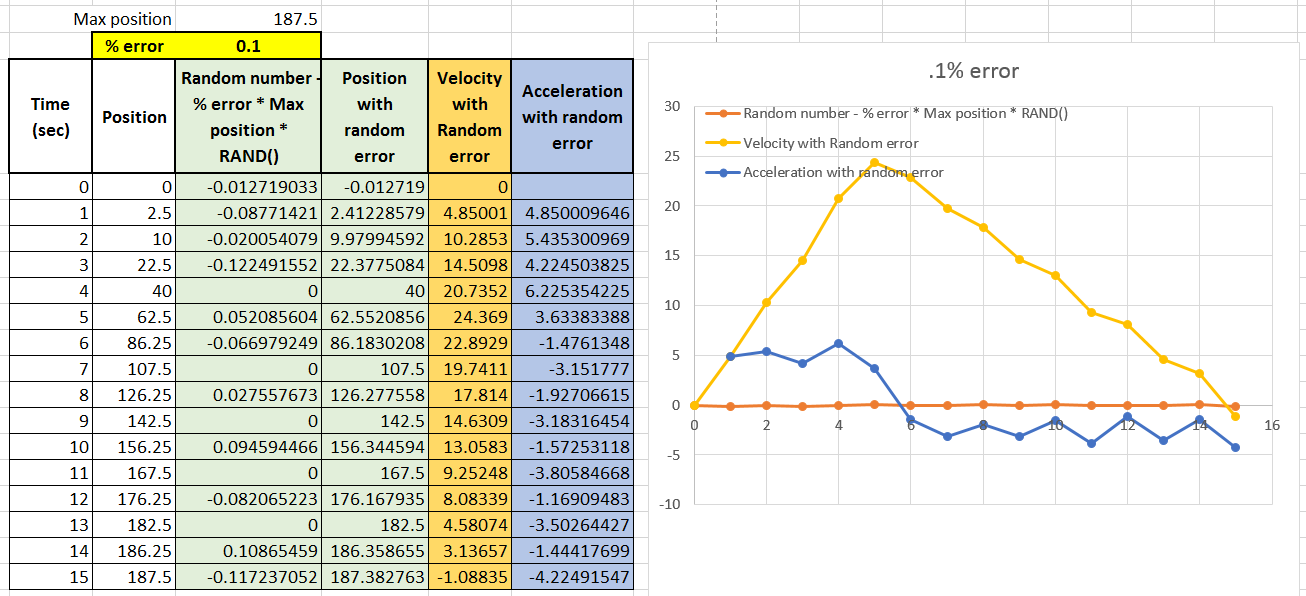
Create a random error using excel's random # generator, then add this random error to the position data. 

$D$4 = Max position

$D$5 = % error  (1)

RAND() = random number generator, generates random numbers between 0 and 1

RANDBETWEEN (-1,1) makes random number either positive or negative

Now - calculate your velocity and acceleration from the data that has random errors, instead of from the perfect position data.

Observe what happens to the velocity and acceleration data as you change the % error that is added in. 

1% error:

Create an xy scatterplot of your velocity and acceleration data, and look at different error values:

0% error:

0.1% error

 1% error

5% error:

Small errors in position = HUGE errors in velocity and acceleration!!!

So, what do we do with imperfect position data?  (Note: the data you take in class will not be perfect, so this is what your initial vel and accelerations will look like)

Try this out:
Fit an equation to your imperfect position data, then create a new column for smoothed position data:

Think about how you can best clean up messy data - then save this spreadsheet, and use it to input your real mousetrap car data!

Note: you might have to create a new smoothed line for your best guess at Vel too...

Error propagation issues can be a pain!!  Try and get the best data you can off of your video!