Dynamics!

Remember the ENGR flowchart?

18.2 Two major divisions of Dynamics:
1. kinematics
- study of motion without reference to the forces causing the motion

2. kinetics
- relates forces to motion

Newton's Laws of Motion:

1st law:
A body in motion tends to stay in motion.


A body at rest wants to stay at rest.


ie - things want to keep doing what they are doing, you have to apply a force if you want it to change what it is doing.

Inertia = the resistance of any physical object to any change in its motion



2nd law: Force = Mass * acceleration
The acceleration of a particle is proportional to the force acting on it and inversely proportional to the particle mass; the direction of acceleration is the same as the force direction.

Large m, Large F.... small F, small m

F = ma
Constant acceleration


3rd law:
The forces of action and reaction between contracting bodies are equal in magnitude, opposite in direction, and colinear.

Law of gravitation:
The force of attraction between two bodies is proportional to the product of their masses and inversely proportional to the square of the distance between their centers.

 

Kinematics:

If position changes linearly with time...


If position changes non-linearly with time:

 

 or - 

x(t) = V.t + 0.5at^2

acceleration = change in velocity / change in time
a = 110/4 = 27.5 ft/s^2

x(0→4) = 0 + 0.5*a*t^2 = 0.5*27.5*4^2 = 220 ft

x(4→6) = V.*t + 0 = 110*(10-4) = 660 ft


Try setting up an excel file that calculates:

• distance, 
• velocity, 
• acceleration. 

Find the area under the curve between times "t1" and "t2". 

Area = triangle + rectangle

V2 = 2*(x2-x1)/(t2-t1) - V1

a = (v2-v1)/(t2-t1)

If you only had the distance and time data below, could you figure out the velocity and acceleration?

Accelerating to top speed from t = 0 to 4 sec
velocity is increasing with time.


Constant Velocity, from t = 0 to 10 sec
Velocity = slope = dx/dt

Displacement for time = 0 to 10 sec

Velocity
Area under curve = (Velocity)*(time)
                            = (feet/sec) * (seconds)
                            = feet
                            = distance traveled

Acceleration
Area under curve = (feet/sec^2) * (sec)
                            = (feet/sec)
                            = change in velocity

Mousetrap Car!!!

Can you figure out what the position, velocity, and acceleration graphs look like for a mousetrap car?

If you want, you could use your acceleration data to calculate some forces (but I won't make you for this lab, we'll just worry about s,V,a)

 Practice problem:

*************************************

Lab:
Collect displacement vs. time data by videotaping your mousetrap car.

Calculate velocities and accelerations from your position vs. time data.

Dynamics lab:
You will only need to write up the results section of this lab report, which includes:

•  x(t), v(t) and a(t) graphs
•  (Use an xy scatter plot, and label the x and y axes.)
•  your video
• your data
• example error propagation calculations.

Last year's video link

Some example data sets:

time (seconds) #1 time displacement (ft) 7.33 0 0 7.77 0.44 1 8.03 0.7 2 8.25 0.92 3 8.4 1.07 4 8.6 1.27 5 8.8 1.47 6 9 1.67 7 9.27 1.94 8 13.8 0 0 14.37 0.57 1 14.65 0.85 2 14.93 1.13 3 15.1 1.3 4 15.35 1.55 5 15.65 1.85 6 15.8 2 7 16.13 2.33 8 16.47 2.67 9 16.77 2.97 10 17.1 3.3 11 28.7 0 0 29.27 0.57 1 29.63 0.93 2 29.9 1.2 3 30.1 1.4 4 30.4 1.7 5 30.57 1.87 6 30.8 2.1 7 31.17 2.47 8
tu: Time (sec) t Distance (feet) 4.4 0 0 4.6 0.2 1 4.9 0.5 2 5 0.6 3 5.07 0.67 4 5.3 0.9 5 5.5 1.1 6 5.6 1.2 7 5.77 1.37 8 6 1.6 9 6.2 1.8 10
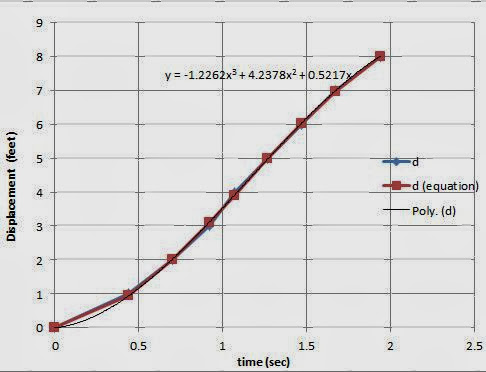
The data isn't perfect, it's better to calculate everything from a fit to the line, instead of from the data itself:
t d d (equation) V V equation a 0 0 0 0 0 0.44 1 0.945533459 4.297879 3.481984 7.9136 0.7 2 2.0211254 3.975905 4.75055 4.8791 0.92 3 3.112010694 5.941234 5.366176 2.7983 1.07 4 3.907928493 4.671003 5.5453285 1.19435 1.27 5 4.985979385 6.109506 5.4807485 -0.3229 1.47 6 6.029308517 4.323785 5.0693685 -2.0569 1.67 7 6.979058289 5.173712 4.3111885 -3.7909 1.94 8 8.008525019 2.451967 2.737534 -5.82835
Use excel to find an equation to your line - right click on line on graph - add trendline - choose polynomial, display equation.